codeforces 569 D. Symmetric and Transitive (组合数学 第二类斯特林数 贝尔数)
D. Symmetric and Transitive
time limit per test
1.5 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
Little Johnny has recently learned about set theory. Now he is studying binary relations. You've probably heard the term "equivalence relation". These relations are very important in many areas of mathematics. For example, the equality of the two numbers is an equivalence relation.
A set ρ of pairs (a, b) of elements of some set A is called a binary relation on set A. For two elements a and b of the set A we say that they are in relation ρ, if pair
, in this case we use a notation
.
Binary relation is equivalence relation, if:
1. It is reflexive (for any _a_ it is true that 
);
2. It is symmetric (for any a, b it is true that if
, then
);
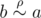3. It is transitive (if
and
, than
).
Little Johnny is not completely a fool and he noticed that the first condition is not necessary! Here is his "proof":
Take any two elements, a and b. If
, then
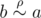(according to property (2)), which means
(according to property (3)).
It's very simple, isn't it? However, you noticed that Johnny's "proof" is wrong, and decided to show him a lot of examples that prove him wrong.
Here's your task: count the number of binary relations over a set of size n such that they are symmetric, transitive, but not an equivalence relations (i.e. they are not reflexive).
Since their number may be very large (not 0, according to Little Johnny), print the remainder of integer division of this number by 109 + 7.
Input
A single line contains a single integer n (1 ≤ n ≤ 4000).
Output
In a single line print the answer to the problem modulo 109 + 7.
Sample test(s)
input
1
output
1
input
2
output
3
input
3
output
10
Note
If n = 1 there is only one such relation — an empty one, i.e.
. In other words, for a single element x of set A the following is hold:
.
If n = 2 there are three such relations. Let's assume that set A consists of two elements, x and y. Then the valid relations are
,ρ = {(x, x)}, ρ = {(y, y)}. It is easy to see that the three listed binary relations are symmetric and transitive relations, but they are not equivalence relations.
给出n个元素的集合上满足传递律，交换律，但不满足自反律的二元关系个数．
还以为是我离散数学没认真听才没做出来．．．
题解：http://blog.csdn.net/mengzhengnan/article/details/47424295
/*************************************************************************
> File Name: code/cf/#315/D.cpp
> Author: 111qqz
> Email: rkz2013@126.com
> Created Time: 2015年08月15日 星期六 06时01分22秒
************************************************************************/
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<string>
#include<map>
#include<set>
#include<queue>
#include<vector>
#include<stack>
#define y0 abc111qqz
#define y1 hust111qqz
#define yn hez111qqz
#define j1 cute111qqz
#define tm crazy111qqz
#define lr dying111qqz
using namespace std;
#define REP(i, n) for (int i=0;i<int(n);++i)
typedef long long LL;
typedef unsigned long long ULL;
const int inf = 0x7fffffff;
const int MOD=1E9+7;
const int N=4E3+5;
LL dp[N][N],c[N][N];
void init()
{
dp[0][0] = 1;
dp[1][1] = 1;
for ( int i = 2; i < N; i++)
{
dp[i][1] = dp[i-1][i-1];
for ( int j = 2 ; j <= i ; j++)
{
dp[i][j] = (dp[i][j-1] + dp[i-1][j-1]) %MOD;
}
}
for ( int i = 1 ; i< N ;i++)
{
c[i][0] = 1;
c[i][i] = 1;
for ( int j = 1 ; j<i ; j++)
{
c[i][j] = (c[i-1][j-1] + c[i-1][j])%MOD;
}
}
}
int main()
{
init();
int n;
int ans = 0;
scanf("%d",&n);
for ( int i = 0 ; i < n ; i++)
{
ans = ans + c[n][i] * dp[i][i];
ans = ans % MOD;
}
cout<<ans<<endl;
return 0;
}