codeforces #341 div2 C. Wet Shark and Flowers

Feb 1, 2016 · 4 min read · math 概率

http://codeforces.com/contest/621/problem/C

C. Wet Shark and Flowers

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

There are n sharks who grow flowers for Wet Shark. They are all sitting around the table, such that sharks i and i + 1 are neighbours for all i from 1 to n - 1. Sharks n and 1 are neighbours too.

Each shark will grow some number of flowers s__i. For i-th shark value s__i is random integer equiprobably chosen in range from _l__i_to r__i. Wet Shark has it's favourite prime number p, and he really likes it! If for any pair of neighbouring sharks i and j the product s__i·s__j is divisible by p, then Wet Shark becomes happy and gives 1000 dollars to each of these sharks.

At the end of the day sharks sum all the money Wet Shark granted to them. Find the expectation of this value.

Input

The first line of the input contains two space-separated integers n and p (3 ≤ n ≤ 100 000, 2 ≤ p ≤ 109) — the number of sharks and Wet Shark's favourite prime number. It is guaranteed that p is prime.

The i-th of the following n lines contains information about i-th shark — two space-separated integers l__i and r__i(1 ≤ l__i ≤ r__i ≤ 109), the range of flowers shark i can produce. Remember that s__i is chosen equiprobably among all integers from_l__i_ to r__i, inclusive.

Output

Print a single real number — the expected number of dollars that the sharks receive in total. You answer will be considered correct if its absolute or relative error does not exceed 10 - 6.

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if .

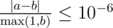Sample test(s)

input

3 2
1 2
420 421
420420 420421

output

4500.0

input

output

0.0

Note

A prime number is a positive integer number that is divisible only by 1 and itself. 1 is not considered to be prime.

Consider the first sample. First shark grows some number of flowers from 1 to 2, second sharks grows from 420 to 421flowers and third from 420420 to 420421. There are eight cases for the quantities of flowers (_s_0, _s_1, _s_2) each shark grows:

  1. (1, 420, 420420): note that _s_0·_s_1 = 420, _s_1·_s_2 = 176576400, and _s_2·_s_0 = 420420. For each pair, 1000 dollars will be awarded to each shark. Therefore, each shark will be awarded 2000 dollars, for a total of 6000 dollars.
  2. (1, 420, 420421): now, the product _s_2·_s_0 is not divisible by 2. Therefore, sharks _s_0 and _s_2 will receive 1000 dollars, while shark _s_1 will receive 2000. The total is 4000.
  3. (1, 421, 420420): total is 4000
  4. (1, 421, 420421): total is 0.
  5. (2, 420, 420420): total is 6000.
  6. (2, 420, 420421): total is 6000.
  7. (2, 421, 420420): total is 6000.
  8. (2, 421, 420421): total is 4000.

The expected value is .

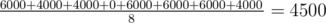In the second sample, no combination of quantities will garner the sharks any money.

题意：有n个区间，第i个和第i+1个相邻，特别地，第n个和第1个也是相邻的。每个区间选择每个数的可能性是相同的。如果一个组相邻区间选到的两个数的乘积可以被给定的素数p整除，那么这两个区间各得2000分，问所有区间的得分的期望总和是多少。

思路：如果乘积是能被p整除，那么这两个数中至少有一个能被p整除。

而这两个数具体是多少我是不关心的。。我们只关心它能不能被p整除。

由加法原理，期望总和等于所有组相邻的区间的期望之和。

**对于任意一组相邻区间，两个数的乘积能整除p有三种情况。。。比较复杂。。不妨考虑反面。即两个数都不能被p整除。 **

如果我们能够统计出每个区间内能被p整除的数的个数，这个概率就可以求出来了。

而对于任意一个区间，[l,r]，直接统计能被p整除似乎有些困难，需要分情况讨论。

我们不妨从初始划分。将区间[l,r]分成[1,l-1]和[1,r] 1到x中能被p整除的数的个数为x/p.

所以区间[l,r]中能被p整除的个数为 r/p-(l-1)/p;(考虑这种方法的一般意义，即如果要统计某个区间的某种数量，正面直接难统计的话，我们可以间接来统计，可能是从1，也可能是从0)

需要注意的是：对于输出绝对误差/相对误差不超过1E-x的输出要求。。。保留的小数位至少要x+2位才比较保险。。。。。

/* ***********************************************
Author :111qqz
Created Time :2016年01月31日 星期日 22时02分47秒
File Name :code/cf/#341/C.cpp
************************************************ */

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <string>
#include <cmath>
#include <cstdlib>
#include <ctime>
#include <iomanip>
#define fst first
#define sec second
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define ms(a,x) memset(a,x,sizeof(a))
typedef long long LL;
#define pi pair < int ,int >
#define MP make_pair

using namespace std;
const double eps = 1E-8;
const int dx4[4]={1,0,0,-1};
const int dy4[4]={0,-1,1,0};
const int inf = 0x3f3f3f3f;
const int N=1E5+7;
int n ;
int p;
int l[N],r[N];
double len[N];
double cnt[N];
int main()
{
	#ifndef  ONLINE_JUDGE 
	freopen("code/in.txt","r",stdin);
  #endif
	cin>>n>>p;
	ms(cnt,0);
	ms(len,0);
	for ( int i = 0 ;i  < n ; i++)
	{
	    scanf("%d %d",&l[i],&r[i]);
	    len[i] = r[i]-l[i]+1;
	}

	for ( int i = 0 ;i  < n ; i++)
	{
	   cnt[i] = r[i]/p - (l[i]-1)/p;
	}
	double sum = 0 ;
//	for ( int i = 0 ;i < n ; i++) cout<<cnt[i]<<endl;
	for ( int i = 0 ; i < n ; i++)
	{
	    int j = (i+1)%n;
	    sum +=1- ((len[i]-cnt[i])/len[i]*1.0)*((len[j]-cnt[j])/len[j]*1.0);
	}
	cout<<fixed<<setprecision(6)<<sum*2000<<endl;  //输出不保留足够的小数位就为产生更大的误差。
	//printf("%.8lf\n",sum*2000);

	


  #ifndef ONLINE_JUDGE  
  fclose(stdin);
  #endif
    return 0;
}