codeforces 455 E. Function (斜率优化，线段树套凸包)
题目链接 题意：已知 f(1, j) = a[j] f[i][j] = min (f[i-1][j],f[i-1][j-1]) 然后给出 n n≤1E5 个数（a[i] ai≤1E4)，给出 m组查询（m<=1E5），每组两个数 x,y 问 f(x,y) 是多少。
参考题解：茶姐的回答（下标好像搞错了，领会意思即可
以及前置技能点是：斜率优化+线段树
思路：考虑一排数a[1]到a[n]，原问题可以转化成从a[y]走x-1步，每一步原地不动或者向左移动一个格子后的总的代价。
Function is calculated as follows:
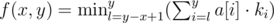, k__i — how many times we visited the i th element of the array a.
这个式子感觉不是很明确。。。。
窝来解释一下。。。l=y-x+1是可能走到的最左边的点。。。。
终点在【L,Y】区间内都是合法的。。。。
然后考虑代价最小的情况。。。
一定是在最小的格子上尽可能多得停留，在其他格子上只停留一次。。。
对于终点为l的情况，走到y要花费y-l步,一共要走x-1步，那么多出来x-1-(y-l)步，这些步停留在最小的点上是最优的，最小的点上之前停留了一次，现在再多停留x-1-(y-l)次，也就是停留了x-(y-l)次。
那么，另一个结论是，区间[l,y]中，当a[l]为最小的时候才是最优的。。。
为什么呢？
假设a[k] (k>l)是最小，那么以a[k]为终点的情况一定比以a[l]为终点的情况优秀（因为多走了【l,k-1】之间的点。。。走这些点比停留在a[k]的代价大）
因此对于l是终点的情况，一定在a[l]是最小值的时候是最优的。
此时代价为：
sum[y] - sum[l] + a[l]·(x - (y - l))
我们变形得到：
sum[y] - sum[l] + a[l]·(x - (y - l)) = sum[y] - sum[l] + a[l]·(x - y + l) = sum[y] - sum[l] + a[l]·l + a[l]·(x - y) = sum[y] + (a[l]·(x - y) + a[l]·l - sum[l])
观察发现这似乎有斜率的样子...
You may notice that in brackets something like the equation of the line — _K_·_X_ + _B_. That's very similar to the equation of the line:_a_[_l_]·(_x_ - _y_) + _a_[_l_]·_l_ - _sum_[_l_], where _K_ = _a_[_l_], _X_ = (_x_ - _y_), _B_ = _a_[_l_]·_l_ - _sum_[_l_].Now we must find minimum for all l and fixed X = (x - y).
We have n lines, i. e. for every element in array a one line (K__i, B__i).
Answer for query equal to:
, where (K__i, B__i) — i-th line. K__i = a[i], B__i = a[i]·i - sum[i].
For fast answer calculation we must use Convex Hull Trick with segment tree. In every vertex of segment tree we keep all lines for segment of this vertex. This requires
space, because each line lies in
vertices. And we can answer query in
operations. Because we visit
vertices and each vertex need in
关于斜率优化（convex hull trick）的进一步讲解
Remainder: convex hull trick lets us maintain _k_ linear functions of the form _f__i_(_x_) = _a__ix_ + _b__i_ and answer efficiently (in time proportional to number of functions) to the queries _Q_(_x_) = _min_1 ≤ _i_ ≤ _k_ _f__i_(_x_) (given _x_).Now we will be able to solve the problem if we can answer a bit more general kind of queries: we consider only lines with indices from given L and R; formally, Q(x, L, R) = min__L ≤ i ≤ R f__i(x).
How can we do it? Let's make a segment tree! Let's say we have such m that 2_m_ ≥ n. Then the root contains the convex hull of lines having indices [0, 2_m_ - 1], its left child contains [0, 2_m_ - 1 - 1], right child [2_m_ - 1, 2_m_ - 1]and so on. We can costruct all these hulls one by one; without any optimizations it gives us time
.
Now let's say we have to answer the query Q(x, L, R). Then we just "break" the interval [L, R] into base intervals (in the same way a segment tree does) and for each of
What's the time? We have
第一次写线段树套凸包，虽然线段树窝会写，斜率优化的思想我也明白，不过套在一起如何实现还是参考了不少别人的写法。
/* ***********************************************
Author :111qqz
Created Time :Sun 25 Sep 2016 10:50:45 PM CST
File Name :code/cf/problem/455E.cpp
************************************************ */
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <string>
#include <cmath>
#include <cstdlib>
#include <ctime>
#define fst first
#define sec second
#define lson l,m,(rt<<1)+1
#define rson m+1,r,(rt<<1)+2
#define ms(a,x) memset(a,x,sizeof(a))
typedef long long LL;
#define pi pair < int ,int >
#define MP make_pair
using namespace std;
const double eps = 1E-8;
const int dx4[4]={1,0,0,-1};
const int dy4[4]={0,-1,1,0};
const int inf = 0x3f3f3f3f;
const int maxn = 1E5+7;
long double intersect(int k, int b, int kk, int bb) {
return (long double)(b - bb) / (kk - k);
}
struct ConvexHull {
int * k, * b;
int len;
ConvexHull() : k(0), b(0), len(0) {}
void addLine(int kk, int bb) {
if (len == 1 && k[len - 1] == kk) {
bb = max(b[len - 1], bb);
len = 0;
}
if (len <= 1) {
k[len] = kk;
b[len] = bb;
len++;
return;
}
while (len >= 2 && ((k[len - 1] == kk && b[len - 1] > bb) || (kk != k[len - 1] && intersect(k[len - 2], b[len - 2], k[len - 1], b[len - 1]) >= intersect(k[len - 1], b[len - 1], kk, bb)))) len--;
while (len >= 1 && k[len - 1] == kk && b[len - 1] > bb) len--;
if (len >= 1 && k[len - 1] == kk && b[len - 1] <= bb) return;
k[len] = kk;
b[len] = bb;
len++;
}
int get(int idx, int x) {
return k[idx] * x + b[idx];
}
bool f(int idx, int x) {
return get(idx, x) >= get(idx + 1, x);
}
int getMin(int x) {
int l = -1, r = len - 1;
while (r - l > 1) {
int mid = (l + r) >> 1;
if (f(mid, x)) l = mid;
else r = mid;
}
return get(r, x);
}
};
int n, q, a[maxn], s[maxn];
ConvexHull t[maxn * 4];
void mergeCHs(ConvexHull & res, ConvexHull & a, ConvexHull & b) {
res.len = 0;
res.k = new int[a.len + b.len];
res.b = new int[a.len + b.len];
int l = 0, r = 0;
while (l + r != a.len + b.len)
if (l == a.len) {
res.addLine(b.k[r], b.b[r]);
r++;
}
else if (r == b.len) {
res.addLine(a.k[l], a.b[l]);
l++;
}
else if (a.k[l] > b.k[r]) {
res.addLine(a.k[l], a.b[l]);
l++;
}
else {
res.addLine(b.k[r], b.b[r]);
r++;
}
}
void PushUp( int rt)
{
mergeCHs(t[rt],t[(rt<<1)+1],t[(rt<<1)+2]);
}
void build ( int l,int r,int rt)
{
if (l==r)
{
t[rt].k = new int[1];
t[rt].b = new int[1];
t[rt].k[0] = a[l];
t[rt].b[0] = a[l] * l - s[l];
t[rt].len = 1;
return;
}
int m = (l+r)>>1;
build(lson);
build(rson);
PushUp(rt);
}
int query(int L,int R,int x,int l,int r,int rt)
{
if (L<=l&&r<=R) return t[rt].getMin(x);
int m = (l+r)>>1;
int ret = inf;
if (L<=m) ret = min(ret,query(L,R,x,lson));
if (R>=m+1) ret = min(ret,query(L,R,x,rson));
return ret;
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("code/in.txt","r",stdin);
#endif
scanf("%d",&n);
s[0] = 0 ;
for ( int i = 1 ; i <= n ; i++) scanf("%d",&a[i]),s[i] = s[i-1] + a[i];
build(1,n,0);
int q;
scanf("%d",&q);
while (q--)
{
int x,y;
scanf("%d%d",&x,&y);
printf("%d\n",s[y] + query(y-x+1,y,x-y,1,n,0));
}
#ifndef ONLINE_JUDGE
fclose(stdin);
#endif
return 0;
}