codeforces 501 D Misha and Permutations Summation (康托展开+康托逆展开+factorial_number_system+线段树×2)
题意：给出两个排列，定义ord(p)为排列p的顺序（字典顺从小到大），定义perm(x)为顺序为x的排列，现在要求
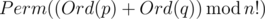1 ≤ n ≤ 200 000
思路：首先去学了一下康托展开和逆展开。。。其实就是对于这种排列之类的问题。。。的一个比较省空间的hash函数。。。？
然后由于n非常大。。康托展开中要查找当前位置后面有多少个比当前位置小的。。。
然而这复杂是n2。。。肯定gg。。。
因此里面那层我们用一课线段树维护。。。复杂度nlgn
在康托逆展开的过程中。。。我们要查询之前没有出现过的第k个元素。。。。
因为n很大这里也需要线段树来维护。。。
所以再建一棵线段树。。。某位置表示初始时刻是否为空，初始都为1，表示都没有出现。思想类似于poj 2828 poj 2828解题报告
然后还是由于n很大。。。在康托展开中的阶乘部分。。。完全存不下。。。
直接用高精度应该也能做？
不过比较推荐的做法是： The Factorial Number System wiki_Factorial number system
是一种和阶乘相关的进制表示法。
大概就是不同位置上的权值，不像一般的k进制数，是k^0,k^1,k^2....
而是0!,1!,2!。。。
这种表示合法的正确性基于：
1*1! + 2*2! + 3*3! + ... + k*k! = (k+1)! - 1
具体参见上面两个链接。
因为我们可以把所有康托展开都用 Factorial number system来表示。
1/* ***********************************************
2Author :111qqz
3Created Time :Tue 13 Sep 2016 04:33:55 PM CST
4File Name :code/cf/problem/501D.cpp
5************************************************ */
6#include <cstdio>
7#include <cstring>
8#include <iostream>
9#include <algorithm>
10#include <vector>
11#include <queue>
12#include <set>
13#include <map>
14#include <string>
15#include <cmath>
16#include <cstdlib>
17#include <ctime>
18#define fst first
19#define sec second
20#define lson l,m,rt<<1
21#define rson m+1,r,rt<<1|1
22#define ms(a,x) memset(a,x,sizeof(a))
23typedef long long LL;
24#define pi pair < int ,int >
25#define MP make_pair
26using namespace std;
27const double eps = 1E-8;
28const int dx4[4]={1,0,0,-1};
29const int dy4[4]={0,-1,1,0};
30const int inf = 0x3f3f3f3f;
31const int N=2E5+7;
32int n ;
33int tree[N<<2];
34int fac[N];
35int A[N],B[N];
36int ans[N];
37void PushUp(int rt)
38{
39 tree[rt] = tree[rt<<1] + tree[rt<<1|1];
40}
41void update(int p,int l,int r,int rt)
42{
43 if (l==r)
44 {
45 tree[rt]++;
46 return;
47 }
48 int m = (l+r)>>1;
49 if (p<=m) update(p,lson);
50 else update(p,rson);
51 PushUp(rt);
52}
53int query(int L,int R,int l,int r,int rt)
54{
55 if (L<=l&&r<=R) return tree[rt];
56 int m = (l+r)>>1;
57 int ret = 0 ;
58 if (L<=m)
59 {
60 int res = query(L,R,lson);
61 ret +=res;
62 }
63 if (R>=m+1)
64 {
65 int res = query(L,R,rson);
66 ret +=res;
67 }
68 return ret;
69}
70void Contor(int A[])//https://en.wikipedia.org/wiki/Factorial_number_system
71{
72 ms(tree,0);
73 for ( int i = 0 ; i < n ; i++)
74 {
75 int x;
76 scanf("%d",&x);
77 x++;
78 A[n-i-1] = x-query(1,x,1,n,1)-1; //A[i]位置是factorial_number_system所表示的高精度，整个A数组表示contor展开的答案（也就是字典序第几大），具体参考上面的链接。
79 update(x,1,n,1);
80 }
81}
82void print(int *a,int n)
83{
84 for ( int i = 0; i < n ; i++ ) printf("%d ",a[i]);
85 printf("\n");
86}
87void build( int l,int r,int rt)
88{
89 if (l==r)
90 {
91 tree[rt] = 1; //第二棵线段树。。。表示的是空位置的个数。。。初始每个节点都为空，所以都为1.
92 return;
93 }
94 int m = (l+r)>>1;
95 build(lson);
96 build(rson);
97 PushUp(rt);
98}
99int update2( int x,int l,int r,int rt)
100{
101 if (l==r)
102 {
103 tree[rt]--;
104 return l;
105 }
106 int m = (l+r)/2;
107 int ret ; //又犯了。。。递归多层只由最后一层返回结果的错误2333，
108 if (x<=tree[rt<<1]) ret = update2(x,lson);
109 else ret =update2(x-tree[rt<<1],rson);
110 PushUp(rt);
111 return ret;
112}
1void ni_Contor()
2{
3 build(1,n,1);
4 A[0] = 0 ;
5 for ( int i = n -1 ; i>= 0 ; i--)
6 {
7 int x =update2(A[i]+1,1,n,1)-1;
8 printf("%d%c",x,i==0?'\n':' ');
9 }
10}
11int main()
12{
13 #ifndef ONLINE_JUDGE
14 freopen("code/in.txt","r",stdin);
15 #endif
16 cin>>n;
17 Contor(A); //读入排列p并且将其康托展开，然后按照factorial_number_system存入A数组。
18 Contor(B);
19// print(A,n);
20// print(B,n);
21 int tmp = 0 ;
22 for ( int i = 1 ; i < n ; i++) //
23 {
24 A[i]+=B[i]+tmp; //这部分就是在factorial_number_system下求A和B两个数的和%n!...只不过是每一步分别算了。。。
25 tmp = A[i]/(i+1);
26 A[i]-=tmp*(i+1); //处理了高精度的进位和%运算。
27 }
28// print(A,n);
29 ni_Contor();
1 #ifndef ONLINE_JUDGE
2 fclose(stdin);
3 #endif
4 return 0;
5}