hdu 4335 What is N? (指数循环节+欧拉函数)
题意:给出b,p,m(( 0<=b<P, 1<=P<=10^5, 1 <= M <=2^64 – 1 )),问满足图中条件的n有多少个。
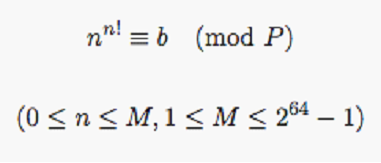
思路:这题由于对p没有限制,所以细节多一些,需要讨论。
首先我们知道指数循环节公式,也就是所谓的降幂公式为:a^x = a^(x mod phi(c)+phi(c)) (mod c) x>=phi(c),(ps:后面的限制条件,在x<phi(c)的时候,该式子依然正确,只不过增加了运算复杂度。。。? 存疑)
然后我们只需要对n分两种情况讨论。
第一种是n<t ,第二种是n>=t (t = min{x| x! % phi(P)==0})
由于t不会很大。。前一种直接暴力。。。
后一种用降幂公式搞之。。。
1/* ***********************************************
2Author :111qqz
3Created Time :Thu 27 Oct 2016 03:43:05 AM CST
4File Name :code/hdu/4335.cpp
5************************************************ */
6#include <cstdio>
7#include <cstring>
8#include <iostream>
9#include <algorithm>
10#include <vector>
11#include <queue>
12#include <set>
13#include <map>
14#include <string>
15#include <cmath>
16#include <cstdlib>
17#include <ctime>
18#define fst first
19#define sec second
20#define lson l,m,rt<<1
21#define rson m+1,r,rt<<1|1
22#define ms(a,x) memset(a,x,sizeof(a))
23typedef long long LL;
24#define pi pair < int ,int >
25#define MP make_pair
26typedef unsigned long long ULL;
27using namespace std;
28const double eps = 1E-8;
29const int dx4[4]={1,0,0,-1};
30const int dy4[4]={0,-1,1,0};
31const int inf = 0x3f3f3f3f;
32const int N =2E5+7;
33LL b,p;
34LL a[N];
35unsigned long long M;
36LL euler( LL x)
37{
38 LL ret = 1;
39 for ( LL i = 2 ; i * i <= x ; i++)
40 {
41 if (x%i==0)
42 {
43 x/=i;
44 ret*=(i-1);
45 while (x%i==0)
46 {
47 x/=i;
48 ret*=i;
49 }
50 }
51 }
52 if (x>1) ret*=(x-1);
53 return ret;
54}
55LL ksm( LL a,LL b,LL k)
56{
57 LL res = 1;
58 while (b>0)
59 {
60 if (b&1) res = (res * a) % k;
61 b = b >> 1LL;
62 a = (a*a) % k;
63 }
64 return res;
65}
66int main()
67{
68 #ifndef ONLINE_JUDGE
69 freopen("code/in.txt","r",stdin);
70 #endif
71 int T;
72 cin>>T;
73 int cas = 0;
74 while (T--)
75 {
76 scanf("%lld%lld%llu",&b,&p,&M);
77 printf("Case #%d: ",++cas);
78 LL mod = euler(p);
79 if (p==1)
80 {
81 if (b==0)
82 {
83 if (M==18446744073709551615ULL)
84 puts("18446744073709551616");
85 else printf("%llu\n",M+1); //把%llu 写成了%lld...wa了半天。。。。。<sad
86 }else printf("0\n");
87 continue;
88 }
89 LL cnt = 0 ;
90 LL fac = 1;
91 LL i = 0 ;
92 /*
93 for ( i = 0 ; ULL(i)<=M&&fac < mod ; i++)
94 {
95 if (ksm(i,fac,p)==b) cnt++;
96 fac *= (i+1);
97 }
98 */
99 fac%=mod;
100 for ( ; ULL(i)<=M && fac ; i++)
101 {
102 if (ksm(i,fac+mod,p)==b) cnt++;
103 fac = fac*(i+1)%mod;
104 }
105 if (ULL(i)<=M)
106 {
107 LL num = 0 ;
108 for ( int j = 0 ; j < p ; j++)
109 {
110 a[j] = ksm(i+j,mod,p);
111 if (a[j]==b) ++num;
112 }
113 LL bk_num = (M-i+1)/p;
114 cnt +=bk_num*num;
115 LL Rem = (M-i+1)-bk_num*p;
116 for ( int j = 0 ; j < Rem ; j++)
117 cnt += (a[j]==b);
118 }
119 printf("%lld\n",cnt);
120 }
121 #ifndef ONLINE_JUDGE
122 fclose(stdin);
123 #endif
124 return 0;
125}