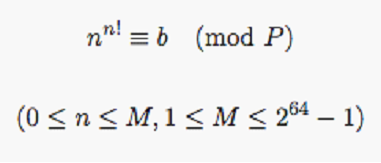指数循环节

题目链接 题意：给出了一段伪代码。分析得知其实就是f[1]= a,f[2] = b,f[n]=f[n-1] * f[n-2] 思路：一眼题，和hdu4549很类似hdu4549解题报告 不同的是这道题中p不一定是质数（其实不是也无所谓啊…hdu4549只不过是因为1E9+7是指数，又用费马小定理化简了一下，这道理%phi(p)即可）

题目链接 题意： Assume that f(0) = 1 and 0^0=1. f(n) = (n)^f(n/10) for all n bigger than zero. Please calculate f(n)%m. (2 ≤ n , m ≤ 10^9, x^y means the y th power of x). 思路：指数循环节。 trick点在于0^0=1这点。 比较容易想到的一层是ksm的时候特判。 比较不容易想到的一层是，0作为底数的时候，可能出现0^a在用降幂公式加速后，出现0^0。

题目链接 题意：给出b,p,m（( 0<=b<P, 1<=P<=10^5, 1 <= M <=2^64 – 1 )），问满足图中条件的n有多少个。 思路：这题由于对p没有限制，所以细节多一些，需要讨论。 首先我们知道指数循环节公式，也就是所谓的降幂公式为：a^x = a^(x mod phi(c)+phi(c)) (mod c) x>=phi(c)，（ps：后面的限制条件，在x<phi(c)的时候，该式子依然正确，只不过增加了运算复杂度。。。？ 存疑）

题目链接 题意：求一个楼梯数%m的大小。 思路：指数循环节。 需要注意的是，模数只有最外层是m，每往里一层，模数都变成m=phi(m) 所以可以写个dfs或者先预处理出每一层m存一下。

题目链接 题意：定义s(k)为将n分成k个正整数的划分数，给出n，问s(1) + s(2) + … + s(n-1) + s(n)是多少，结果9+7，其中n<=10^100000。 思路：首先化简要求的式子。

题意：M斐波那契数列F[n]是一种整数数列，它的定义如下： F[0] = a F[1] = b F[n] = F[n-1] * F[n-2] ( n > 1 ) 现在给出a, b, n，你能求出F[n]的值吗？ 思路：观察发现。。。F[n] = a^(fib(n-1)) * b ^ (fib(n))

资料先行： 指数循环节证明 指数循环节2 对指数循环节的一些理解 挂了一点题目，写完来写总结。 vjudge_不会指数循环节的111qqz 写完了。 首先要注意的是： 首先我们知道指数循环节公式，也就是所谓的降幂公式为：a^x = a^(x mod phi(c)+phi(c)) (mod c) x>=phi(c)，（ps：后面的限制条件，在x<phi(c)的时候，该式子依然正确，只不过增加了运算复杂度。。。？ 存疑）