题目链接 题意：有n扇门，n种钥匙，一一对应。每扇门打开后可能得到k把钥匙（k可能为0）。一扇门还可以用一颗炸弹炸开。现在问要开所有门，使用炸弹的期望个数。 思路：状态压缩。用一个二进制串表示每扇门能打开的门的信息，对应的位上为1表示能打开，为0表示不能打开。 状态是可以传递的。。 如果第i扇门能打开门k，那么能打开第i扇门的第j扇门也可以打开门k。 状态压缩以及传递的过程可以很容易用bitset来维护，这才是bitset的正确打开姿势 相当于用floyd做了一个传递闭包。(floyd的有一层循环隐藏在了bitset中，复杂度没有改变，但是常数小) 最后对于期望的计算方法：统计能打开第i扇门的方案数计为cnt,这cnt的方案中，只有 …

题目链接 题意：n（n<=300）个球，每个球上标有一个标号(a[i]<=300),从中拿一个，不放回，再拿一个，问第一个球上的数字严格大于第二个球上的数字的概率。 思路：古典概型。总数为n*(n-1)/2...然后标号最大300,不妨用cnt[i]统计标号为i的球的个数。从小往大扫一遍cnt,cnt[i]对分子的贡献就是cnt[i]*cur。。cur 为 sum{cnt[1]..cnt[i-1]}; 最后注意将分子除以2，因为有一半是第一个球比第二个球小的情况。 /* *********************************************** Author :111qqz Created Time …

http://acm.hdu.edu.cn/showproblem.php?pid=4336 题意：有n种卡片，买一包干脆面得到第i种卡片的概率是p[i],每包干脆面最多有一张卡片，问收集齐所有卡片要买的干脆面的包数的数学期望。 思路：容斥模板题。1.0/p[i]就是拿到某张卡片需要买的包数的数学期望 注意体会这种具体应用容斥的模拟方法，把1<<n转化成二进制来模拟有1个元素的集合，有2个元素的集合...有n个元素的集合。 核心代码： for ( int msk = 1 ; msk <(1<<n) ; msk++) { double res = 0.0; int bits = 0; for ( int …

http://codeforces.com/problemset/problem/148/D 题意：盒子里有w只白老鼠，b只黑老鼠，公主和魔王轮流取（公主先），先取到白老鼠的人获胜。魔王每次取完以后，盒子中的老鼠会因为吓尿了跑掉一只，跑掉的老鼠不算任何人取的。问公主获胜的概率。 思路：概率dp.. dp[i][j]表示有i只白老鼠，j只黑老鼠的时候公主获胜的概率。 转移方程 1. 公主抽到白老鼠（之后龙不必再抽） 胜率为i/(i+j)*1 2. 公主抽到黑老鼠，龙抽到黑老鼠，跳出一只黑老鼠，胜率为j/(i+j) * (j-1)/(i+j-1) * (j-2)/(i+j-2) * f[i][j-3] (j>=3) 3. …

http://codeforces.com/problemset/problem/107/B 题意：有m个部门，每个部分s[i]个人，HW在第h部门，现在要从这m个部门中挑选包括HW在内的n个人去参加比赛，问被挑选的人中有HW的队友（同部门的人）的概率是多少。如果m个部分的人数不够组成n人的球队，输出-1. 思路：考虑一般情况。至少有一个队友的情况较多，应该从反面考虑，即没有一个队友的情况。选完HW以后面临的状态是：事件总数为从total(m个部门的人员之和)-1个人中选n-1个的方案数，包含的事件数目为从a(a=total-s[h])中选n-1个人包含的方案数。 可以看出分母相同，可以约掉。 然后对于边界情况，首先判断total是 …

http://codeforces.com/problemset/problem/518/D 题意：有n个人排队上一个电梯。。。在某一秒内，队首的人有p的概率上电梯，1-p的概率不动。每个人只有在队首的位置才可以上电梯（也就是每一秒内，最多只有一个人可以上电梯）。电梯无线长（也就是上了电梯就不会离开了），问在第t秒的时候，电梯上的人的个数的数学期望是多少。 思路：一开始推公式的我还是图样。这题是dp.其实也不难想。dp[i][j]表示第i秒时电梯上有j个人的概率。 当j==n的时候，也就是所以人都上了电梯以后。dp[i+1][j]+=dp[i][j], …

http://codeforces.com/problemset/problem/312/B 题意：两个人比赛射箭，先射的人射中的概率是a/b,后射的人射中的概率是c/d,问先射的人赢的概率。 思路：应该叫条件概率。。。？ 不过我们可以用古典概型的思维想。每射一次看成一个点，射中的点用白色表示，没有射中的用黑色表示。如果两个人第i次都没有射中，那么就要继续第i+1 轮，而第i+1轮和之前的每一轮是独立的。等于重复这个过程。所以古典概型的样本总量应该减去宝石两个人都没有射中的点的个数，为bd-(b-a)(d-c)，整理为bc+ad-a*c，设为n.要想第一个人赢，那么对于某一次，只要不是第一个人没射中，第二个人射中这种情况，就都是第一 …

http://codeforces.com/problemset/problem/453/A 题意：m面筛子，每面点数出现的概率相同，连续投掷n次，问出现的最大值的数学期望。 思路：手写样例。。。发现答案为 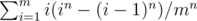。。。记得把（1/m）^n放进去。 观察答案，可以这样理解（我是用样例推出公式后理解。。。数学差的人心好累）：如果i为最大值，那么n次每次必须投掷出1..i的点数，概率为 (i/m)^n,但是要至少有一个投掷成i，也就是要减去所有的数都是1..i-1中的情况（概率 为((i-1)/m)^n）， /* *********************************************** Author :111qqz …

http://codeforces.com/problemset/problem/476/B 题意：给出两个长度相等-且不超过10的字符串，串1只包含‘-’,'+‘。按照‘+’为1，‘-’为-1累加可以得到一个值。串2还包含若干‘？’，代表该处的值不确定，且为'+'和'-'的概率相等，都是0.5.问串2的值和串1相等的概率。 思路：我们可以扫一遍得到‘？’的个数和两个式子的差值。设问号个数为a,差值为b，那么在a个问号中需要有(a-b)/2个为‘+’（容易知道，a,b一定奇偶性相同，所以a-b一定能被2整除），根据超几何分布，概率为 c[a][(a-b)/2]*(1/2)^a; 写的时候可以先打个组合数的表。1A,开心。 /* …

http://codeforces.com/contest/621/problem/C C. Wet Shark and Flowers time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard output There are n sharks who grow flowers for Wet Shark. They are all sitting around the table, such that sharks i and i + 1 are neighbours for all …